[圖論] 生成樹的定義與性質
引言
在圖論中,生成樹是指連接圖中所有頂點且邊數最少的子圖,即此圖連通且邊數最少。**
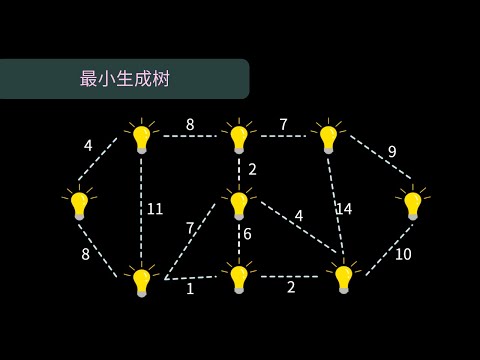

定義
設無向圖 G 的頂點集為 V,邊集為 E。若圖 T 滿足以下條件:
- V(T) = V(G)(T 與 G 具有相同的頂點)
- E(T) ⊂ E(G)(T 的邊數少於 G)
則 T 是圖 G 的生成樹。

性質
生成樹具有以下性質:
| 性質 | 説明 |
|---|---|
| 邊數最小 | 在連接所有頂點的前提下,邊數最少 |
| 連通性 | 圖 T 連接所有頂點 |
| 循環性 | 圖 T 不含任何環路 |
| 唯一性 | G 的生成樹在不考慮邊的標號情況下是唯一的 |
歷史溯源
五行觀念最早見於《尚書·洪範》,提出「五行:水、火、木、金、土」。後世註釋家將五行排列順序與其固有屬性聯繫,認為水最微著為一,火漸著為二,木形實為三,金體固為四,土質大為五。
五行與其他自然屬性的組合形成了系統性的世界模式,包括五時、五方、五音、五色、五味、五臟、五官、五氣、五性、五體、五液等。
《呂氏春秋》的五行數與《尚書·洪範》的五行數有所對應,將原五行數與土數結合,形成新的五行數。楊雄在《太玄·玄數》中強調土為五行之中,指出三八為木、四九為金、二七為火、一六為水,五五為土。
《太玄·玄圖》提出「一與六共宗,二與七為朋,三與八成友,四與九同道,五與五相守」,土挨個兒配四時、四方而無定位,即居中央又影響四方。如此,四時、五行和數字的配合更加協調。
結論
生成樹是圖論中連通圖的不變性質,定義明確,性質清晰,在實際應用中具有重要意義。五行觀念自古有之,經過後世演繹,融入其他自然屬性,形成了系統性的世界觀。
生成數:機器學習模型評估與選擇的關鍵指標
生成數是機器學習模型評估和選擇的關鍵指標。它反映模型的預測能力,並有助於比較不同模型的效能。
什麼是生成數?
生成數是模型對測試資料集所提出的預測與真實標記之間的協調程度測量。它可以採用不同的形式,例如:
- 分類問題:混淆矩陣、ROC 曲線、F1 分數
- 迴歸問題:平均絕對誤差 (MAE)、均方根誤差 (RMSE)、決定係數 (R²)
生成數指標的種類
以下是一些常用於評估生成數的指標:
| 指標 | 描述 |
|---|---|
| 準確率 (Accuracy) | 預測正確的樣本比例 |
| 靈敏度 (Recall) | 正確預測正例的樣本比例 |
| 特異度 (Specificity) | 正確預測負例的樣本比例 |
| F1 分數 | 靈敏度和特異度的調和平均 |
| 平均絕對誤差 (MAE) | 預測值與真實值之間的平均絕對差異 |
| 均方根誤差 (RMSE) | 預測值與真實值之間的平均平方根差異 |
| 決定係數 (R²) | 模型對資料變異的解釋程度 |
如何使用生成數來選擇模型?
使用生成數指標來選擇模型時,請考慮以下因素:
- 問題類型:指標應適用於模型要解決的問題類型(分類或迴歸)。
- 資料特性:考慮資料集的大小、分佈和類別不平衡性。
- 預測目標:確定模型預測的優先順序(例如,高準確率或低誤差)。
- 計算簡便性:選擇易於計算且可解釋的指標。
實際應用範例
以下是一些使用生成數指標來選擇模型的實際應用範例:
- 醫療診斷:選擇能準確區分疾病和健康樣本的模型。
- 金融預測:選擇能預測股票價格或信用風險的模型。
- 客户流失預測:選擇能識別潛在客户流失的模型。
結論
生成數是機器學習模型評估和選擇的關鍵指標。通過理解不同指標的類型、如何使用它們,以及它們在實際應用中的相關性,可以有效地比較和選擇適合特定任務的模型。
延伸閲讀…
生成樹- 維基百科,自由的百科全書
河圖與五行生成數
