[圓錐的底面呈圓形,側面為曲面,由頂點連接到底面圓心的距離為其高度,記為 h。圓錐僅有一條高度。以 V 表示圓柱體積、S 表示圓柱底面積、h 表示圓柱高度,則圓柱體積公式為:
如果體積與高度相等的圓錐和圓柱體積,則圓錐底面積為圓柱底面積的三倍。
如果體積與底面積相等的圓錐和圓柱體積,則圓錐高度為圓柱高度的三倍。
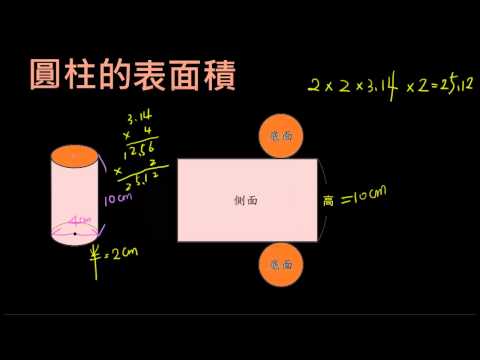

圓柱體與圓錐體不同,圓柱並無頂點的概念,而圓錐則有一個頂點。此外,圓柱具有三個面:側面、兩個底面(圓形),側面為長方形或正方形,且兩個底面相等;圓錐僅有兩個面:側面(扇形)、底面(圓形),僅有一條高度。
對於底面與高度相等的圓柱和圓錐,圓錐體積為圓柱的三分之一,而圓柱體積為圓錐的三倍。]

| 特徵 | 圓柱 | 圓錐 |
|---|---|---|
| 頂點 | 無 | 有 |
| 面數 | 3 | 2 |
| 側面形狀 | 長方形/正方形 | 扇形 |
| 底面形狀 | 圓形 | 圓形 |
| 高度 | 無窮多 | 1 |
| 體積公式 | V = S * h | |
| 等底等高與圓錐體積比 | 3:1 | 1:3 |
圓柱有幾個邊:探索幾何形狀的奧秘
圓柱是三維形狀,其特徵是具有兩個平行且等距的圓形底面,以及連接這些底面的曲面。然而,對於“圓柱有幾個邊”的問題,答案並不簡單。
圓柱的種類與邊數
圓柱的邊數取決於其具體種類,主要有以下幾種:
| 類型 | 邊數 |
|---|---|
| 直圓柱 | 2 個底面圓周 + 曲面圓周 |
| 斜圓柱 | 2 個底面圓周 + 曲面圓周 + 2 個側面矩形 |
| 截圓柱 | 1 個圓底圓周 + 1 個截切圓周 + 截切曲線 |
邊數計算
直圓柱:
對於一個直圓柱,其邊數由兩個底面圓周長和曲面圓周長相加得到:
邊數 = 2πr + 2πr * h
其中:
- r 是底面圓的半徑
- h 是圓柱的高度
斜圓柱:
對於斜圓柱,其邊數在直圓柱的基礎上增加了側面矩形的周長:
邊數 = 2πr + 2πr * h + 2 * 2r * h
截圓柱:
截圓柱的邊數由一個圓底圓周長、一個截切圓周長和截切曲線的長度相加得到。截切曲線的長度取決於截圓柱的截切角度和底面圓的半徑。
