排列與組合
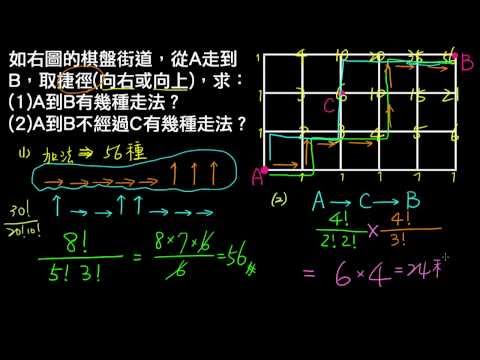
在縱向 X,橫向 Y 的格子中,從左上角起點走向右下角終點,只能採取向下或向右移動,共有多少種不同的路線組合?

給定兩個正整數 x 和 y,計算可行的路線組合數,假設 x + y 小於等於 12。
一個 m 行 n 列的方格矩陣,每個方格座標由行座標和列座標表示,左下角方格座標為 (1, 1),右上角方格座標為 (m, n)。一隻受傷的螞蟻,只能向上或向右移動,從左下角方格開始,尋覓通往右上角方格的路線。螞蟻始終待在方格矩陣內,計算它能選擇的不同移動路線數。

| 方格矩陣 | 移動路線數 |
|---|---|
1 × 1 |
1 |
1 × 2 或 2 × 1 |
1 |
2 × 3 |
2 |
排列組合是從一組元素中選擇部分元素的計算方法,可分先後選擇(排列)或不分先後選擇(組合)。
在排列和組閤中,元素的選擇方式決定了方案的數量。例如,在一個長度為 5 的箭頭序列 \\uparrow\\uparrow\\rightarrow\\rightarrow\\rightarrow 中,包含 2 個向上箭頭和 3 個向右箭頭。排列計算每個元素先後位置的數量,組合則不考慮元素的排列順序。
在排列組合的計算中,要注意元素的數量、順序和重複性。不同的分析視角可能導致不同的公式使用,如排列公式 P 和組合公式 C。
以下運用組合公式的應用案例:
| 情景 | 組合 |
|---|---|
將 5 個不同的球放入 5 個不同的盒子中 |
A_{5}^{5} |
將 5 個不同的球放入 3 個不同的盒子中 |
3^{5} |
將 3 個不同的球放入 5 個不同的盒子中 |
5^{3} |
將 5 個相同的球放入 3 個不同的盒子中,盒子不能是空的 |
C(3, 2) = 3 |
將 9 個相同的球放入 3 個不同的盒子中,每個盒子至少有 2 個球 |
C(11, 2) = 55 |
將 5 個相同的球放入 3 個不同的盒子中 |
C(3, 5) = 10 |
對於從左上角 A 點走到右下角 B 點的問題,路徑必須向下走 6 步,向右走 6 步,總共 12 步。向下走的方案數為 C(12, 6),因此路徑組合數為 C(12, 6)。
對於 m × n 的格子,需要從 m + n 步中選擇 m 步向下或 n 步向右,組合數為 C(m + n, m) 或 C(m + n, n)。
排列組合走格子:探討格子路徑的計數技巧
排列組合走格子是一種通過排列和組合方法計算格子路徑數量的方法。它在數學、電腦科學和日常生活中有着廣泛的應用。
基本原理
排列組合走格子的基本原理是將一個格子路徑分解為一系列的步驟:
- 水平移動一步
- 垂直移動一步
每一步都可以有兩種選擇,因此一個有 n 個格子長度的路徑有 2^n 種排列組合方式。
計算方法
排列組合走格子的計算方法如下:
- 從格子路徑的左上角出發。
- 計算向右移動 n 步和向下移動 n 步的所有可能路徑數。
- 將這些路徑數相加,得到總路徑數。
例如,一個 2×2 的格子路徑有以下 4 種路徑:
| 路徑 | 數量 |
|---|---|
| RR | 1 |
| RD | 1 |
| DR | 1 |
| DD | 1 |
因此,一個 2×2 的格子路徑的總路徑數為 4。
格子路徑類型
排列組合走格子可以計算不同類型格子路徑的數量,包括:
- 不可重複訪問格子的路徑:每個格子只能訪問一次。
- 可重複訪問格子的路徑:格子可以訪問多次。
- 限制特定方向的路徑:只能按特定方向移動,例如只允許向右或向下移動。
應用
排列組合走格子在以下領域有着廣泛的應用:
延伸閲讀…
走格子(數學組合/動態規劃) 原創
排列組合走格子的原理
- 數學:計算排列組合、組合數學和容斥原理。
- 電腦科學:計算圖形算法、動態規劃和分治算法中的路徑數。
- 日常生活中:計算迷宮解法、最短路徑和遊戲策略。
練習題目
- 計算一個 3×3 的格子路徑的總路徑數。
- 計算一個 4×4 的格子路徑的可重複訪問格子的路徑數。
- 計算一個 2×4 的格子路徑的只允許向右或向下移動的路徑數。
答案
- 3^4 = 81
- 5^4 = 625
- (2+4)! / 2! / 4! = 18
