| 樹型態 | 子節點數量(最大) | 數據元素數量(最大) | 葉子節點資料元素數量 | 特徵 |
|---|---|---|---|---|
| 2-3樹 | 3 | 2 | 1-2 | 內部節點可有2或3個子節點 |
| 2-3-4樹 | 4 | 3 | 1-3 | 內部節點可有2、3或4個子節點 |
| 紅黑樹 | 2 | 1 | 1 | 保持黑平衡(所有路徑上的黑色節點數量相同) |
| B樹 | > 2 | 任意 | 任意 | 起始節點除根節點外至少有2個子節點 |
| B+樹 | > 2 | 任意 | 葉子節點儲存所有資料元素,且所有葉子節點深度相同 |
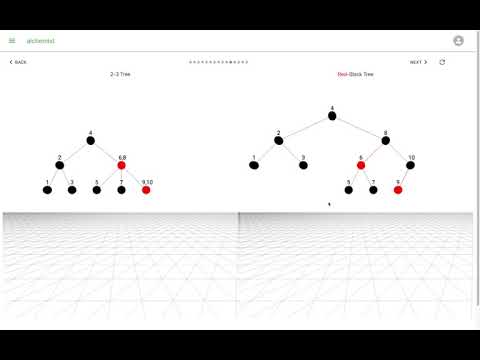
2-3 樹與 2-3-4 樹
2-3 樹是一種平衡樹,允許內部節點最多有 3 個子節點和 2 個數據元素。相似地,2-3-4 樹允許內部節點最多有 4 個子節點和 3 個數據元素。當一個節點需要分裂時,2-3 樹會分裂成兩個 2-3 樹,而 2-3-4 樹會分裂成兩個 2-3-4 樹或 2-3-5 樹。
刪除操作
2-3 樹和 2-3-4 樹的刪除操作涉及以下步驟:

- 尋找:找到包含待刪除元素的節點。
- 合併:如果節點有兩個子節點,將其與一個子節點合併。
- 替換:如果節點有三個子節點,使用其左子樹中最大元素或右子樹中最小元素替換待刪除元素。
- 重平衡:如果節點仍不平衡,則進行重平衡操作,如分裂或合併。
時間複雜度
搜索 2-3 樹和 2-3-4 樹的時間複雜度為 O(log n),其中 n 是樹中的元素數量。插入和刪除操作的時間複雜度也為 O(log n),因為它們需要一次搜索和多次重平衡操作。
優缺點
優點:

- 具有比二叉搜索樹更好的搜索和插入性能。
- 是一種自平衡樹,因此不需要額外的平衡操作。
缺點:
- 比二叉搜索樹更複雜。
- 對於包含大量數據的樹,空間效率可能較低。
2-3樹資料結構
2-3樹是一種平衡搜尋樹,具有以下特性:
- 葉子節點在同一層上。
- 除了根節點,每個節點最多有 3 個子樹。
- 除了根節點,每個子樹最多有 2 個鍵(以下簡稱節點)。
2-3樹的用途包括:
- 儲存和查詢資料
- 用於資料庫和檔案系統
2-3樹插入
在2-3樹中插入一個節點時,可能會發生以下狀況:
- 若節點空間足夠,則直接插入
- 若節點空間不足,則分裂節點並將中鍵提升到父節點
以下為 2-3 樹插入流程的偽代碼:
插入(節點, 鍵值)
若 節點為空
節點.鍵值 = 鍵值
返回
若 節點.鍵值 = 鍵值
跳過
若 節點.鍵數 < 3
插入子樹(節點.左子樹, 鍵值)
或 插入子樹(節點.中子樹, 鍵值)
或 插入子樹(節點.右子樹, 鍵值)
若 節點.鍵數 = 3
分裂節點(節點)
插入子樹(節點, 鍵值)
2-3樹刪除
在2-3樹中刪除一個節點時,可能會發生以下狀況:
- 若節點有 2 個鍵,則可直接刪除
- 若節點有 1 個鍵,則需與鄰近節點合併
以下為 2-3 樹刪除流程的偽代碼:
刪除(節點, 鍵值)
若 節點.鍵值 = 鍵值
若 節點.鍵數 = 2
刪除節點
返回
若 節點.鍵數 = 1
與鄰近節點合併
返回
若 鍵值 < 節點.鍵值
刪除子樹(節點.左子樹, 鍵值)
回補(節點.左子樹)
若 鍵值 > 節點.鍵值
刪除子樹(節點.中子樹, 鍵值)
或 刪除子樹(節點.右子樹, 鍵值)
回補(節點.中子樹或節點.右子樹)
2-3樹時間複雜度
2-3樹的平均搜尋時間為 O(log n)。
2-3樹與 B 樹比較
2-3樹與 B 樹相似,但有以下差異:
| 特徵 | 2-3 樹 | B 樹 |
|---|---|---|
| 度數 | 2 或 3 | M |
| 每個節點的鍵數 | 1 或 2 | B-1 至 M |
| 每個節點的子樹 | 1 或 2 | 最多 M+1 |
B 樹在資料量較大的情況下具有較好的效能。
資料應用
2-3 樹廣泛用於:
延伸閲讀…
三分鐘基礎知識:什麼是2-3 樹?
2-3樹- 算法與複雜度| 小白
- 資料庫中資料索引
- 檔案系統中檔案組織
- 快取和緩衝
